Teacher's Guide: Recursion

Overview

This lesson provides a basic introduction to recursion, an important approach to solving problems that would otherwise require iteration. Students will explore some simple geometric explorations, such as drawing trees, as these can be both instructive and a lot of fun. The lesson also highlights more practical applications, notably using recursion for data validation and analogous tasks. Through the study of recursion, the lesson aims to broaden students' understanding of functions. For example, the lesson's activities encourage students to more closely consider the importance of return statements and the impact of function calls on program flow. Some of the tasks also provide opportunities to practice using callbacks, in particular in conjunction with the Pencil Code read, readnum, and readstr functions.

More about the lesson

In a coding context, recursion provides an alternative to iteration. For certain coding challenges, recursion can offer both shorter and conceptually simpler solutions. This lesson will explore a few of these applications.

However, it's important to acknowledge that while recursion has advantages in some applications, it is very poorly suited for many others. Perhaps the biggest pitfall to recursion is that recursive processes are prone to be inefficient. They can quickly exhaust system memory when used to do tasks that could be trivially solved using iteration. Another obstactle to using recursion is that the logic or recursive algorithms can be hard to understand, and therefore difficult to implement successfully.

All recursive process involves two essential ingredients: (1) a function that can potentially call itself, directly or indirectly, one or more times, and (2) conditional logic that tests whether or not that function self-call should be made. However, the sequencing and timing of these features can significantly impact the behavior of a specific recursive process. Three design considerations are of particular interest: whether the recursion is direct or indirect, tail or non-tail, and single or multiple.

Direct recursion, as the name suggests, results when a function calls itself directly. As a simple example, consider the following script, which generates a countdown on screen.

countdown = (x)->
  cs()
  if x<1  
    # base case
    label "Blast off!", 50  
    return
  label x, 50
  pause 1
  countdown(x-1)  # recursive call

speed 0      
countdown(5)

Indirect recursion (a.k.a. mutual recursion) involves the interaction of two (or more) functions that call each other. The lesson's coding snippet provides and example of indirect recursion. Execution of the askQuestion function invokes the callback cb, which, depending on the test of the base case, may again invoke askQuestion, thereby continuing the recursive process.

Typically, the choice of direct versus indirect recursion is simply one of convenience, readability, or style. For example, the lesson's snippet could equivalently be coded using direct recursion, as follows:

askQuestion = (ans)->
  if ans!=undefined and ans.toLowerCase()=="yes" 
    write "Oh, no!"
    write "We forgot Uncle Steve!"
  else
    readstr 'Are we there yet?', askQuestion
  
askQuestion()

A more significant consideration when writing a recursive function involves the placement of the recursive call within the body of that function. The following snippet (a variation of the lesson's CountDownCountUp activity) provides a simple yet powerful example. By simply reversing the order of the last two statements in the function definitions, the order of the calls to typeline are reversed, changing the functions from counting down to counting up.

countdown = (x)->
  if x<1
    typeline "( countdown's base case was just reached )"
    return
  typeline x
  countdown(x-1) # tail recursion

countdown(5)
    
    
countup = (x)->
  if x<1
    typeline "( countup's based case was just reached )"
    return
  countup(x-1) # non-tail recursion
  typeline x

countup(5)

The countdown function is an example of tail recursion. As the name suggests, the recursive call is the last statement in the function. The countup function, in contrast, is an example of non-tail recursion.

All of the examples encountered thus far in these notes have been of single recursion. Multiple recursion involves making two or more recursive calls within each function. Students will encounter multiple recursion in the lesson through the Tree activity: each call to tree will (potentially) recursively call tree twice, once for each new branch.

The purpose of the base case in recursive functions is to prevent execution of a subsequent call to the recursive function. Without the base case, the recursive process would be infinite. Infinite recursion will quickly consume all available memory allocated to the call stack (discussed in the Technicalities section, below) and the program will crash.

Recursive processes are typically ended by exiting the recursive function. Whether explicitly stated or not, this is done by means of a return statement. Two points noted in the Notes to the Return! lesson are worth remembering here. First, when not explicitly included, return is automatically called when the last line of code in the function is processed. Second, the return value is either the value passed explicitly in the return statement, or, when the return is implicit, the value of the expression generated by the last statement executed in the function.

In the examples and activities given in this lesson, a mix of explicit and implicit return statements have been used. In most cases, the return statement is used solely to exit the function—the value of the return statement is ignored. However, recursive processes are frequently dependent on the value returned., as it is in the following example which computes the sum of the first n counting numbers.

sumToN = (n)->
  if n>1
    return n + sumToN(n-1) 
  return 1 # base case

The algorithm used in sumToN follows an accumulator pattern that is not much different from the algorithm required to code the recursive factorial exercise required for the lesson's Recursion101 activity. This algorithm is rudimentary, as far as recursion goes, but for novices it typically still takes significant effort to comprehend, as the order of execution is essentially reversed from the . The function keeps recursively calling sumToN until the argument is 1. The first return statement to be executed is the base case (return 1). The last return statement to be executed is the one in the initial call to sumToN.

The use of return statements can vary widely across recursive functions. For example, the following recursive function computes the greatest common denominator for two integers a and b using Euclid's algorithm. It may at first blush seem substantially more complicated, but it essentially follows the same recursive pattern as sumToEnd.

gcf = (a,b) ->
  if a>b
    [a,b] = [b,a]
  remainder = b%a
  if remainder==0
    return a # base case
  else
    return gcf(remainder,a)

Notes to activities

CountDownCountUp draws attention to the fact that the order in which you place recursive statements can have significant effects on the output of the process. This same issue features prominently in the BacktrackSpiral activity. The recursive call to sqiral should be placed between calls to rt/fd and bk/lt. As always, students should be advised to start with part of the task (i.e., coding a recursive function that draws a basic spiral) rather than attempt the whole task from the get-go.

There are many potential variations of the Tree program: what angles? how many branches? how much should length change? An additional design consideration is whether to use a single sprite to do the drawing, or to instantiate additional sprites at each branch. The latter approach is facilitated by use of the turtle clone method, as illustrated in this script.

Additional activities

WhileAlternative: Recursive functions offer a functions-based alternative to tackling tasks that might also be solve using while loops. Define and call a recursive function that accomplishes the same output as the following script without using iteration:
```
i=0
c=random($.turtle.colors)
while c != black
  i++
  dot c, 200-2*(i%(200/2-1))
  c=random($.turtle.colors)
```
RecursionInAWord: Write a script that repeatedly prints a phrase to the screen, using smaller and smaller fonts at successively higher positions on the screen. (Alternatively, you might tweak that program so that the small phrases appear first.)
Recursion101: No lesson on recursion would be complete without an assignment to compute factorials. Recall that factorial is defined as n! = n × (n-1) × ... × 2 × 1. For example, 5! = 120. Write a script that contains both iterative and recursive functions that compute factorials for a given integer, e.g., rFactorial and iFactorial. (Note: This is the only activity in the lesson that makes use of return values.)
OralQuiz: Write a script that prompts the user to say a specific word or phrase (e.g., "What's the password?"). Gather this oral input from the user using the Pencil Code listen function. Recursively call listen until the user responds with the correct response.
Validation: Write a script that prompts the user to enter a phone number. Gather this input from the user using the Pencil Code readstr function. After the user enters a value, test that the user entered seven or ten digits. Use recursion to re-prompt the user until they enter a valid number.

Hint: to complete this task, you will need to check a string to see if it has either 7 or 10 numbers. This is a challenge in its own right. One possibility is to use iteration (e.g., a for x in loop) to iterate over the values in the inputted string, testing each character using the typeof function, the isNaN function, or some other technique. Note, however, you could also tackle this sub-task using recursion!
FractalArt: Recursion is well suited to creating fractals, geometric shapes created out of a pattern that repeats (in theory) forever. Search the web for ideas for fractals, or come up with one of your own. Code it using recursion!
MazeEscape: Recursive methods are useful for traversing tree-like data structures. The possible movements in a standard two-dimensional, unicursal maze (i.e., the familiar type of maze in which, on paper, you trace a line between the walls, and which has only one solution) form just such a structure. Hence, recursion is a good tool for solving such a puzzle.

The goal in this activity is to write a program that uses recursion to solve a maze. A straightforward but effective recursive algorithm for navigating a maze is based on "the right-hand rule": put your right hand on the wall and keep it there until you find an exit. (A prerequisite for the right-hand rule to work is that the maze must be "unicursal"; the strategy doesn't work if there are loops in the maze)

Because setting up a maze can be tricky, you might start with this starter code, and focus on writing the recursive function to solve the maze. With this graphics-based maze, in each recursive function call, you should tentitively move into a new space and use touches to test whether it is a valid space or a wall.
SierpinskiTriangle: The Notes to the Chase Other Sprites! lesson include an exercise that introduced students to a means to to construct a Sierpinski Triangle that combined a mix of iteration and randomization. In this activity, construct a Serpinski Triangle deterministically (i.e., without randomness) using recursion. Start with an equilateral triangle of a given color. Divide this triangle into four smaller equilateral triangles, each with a side length half that of the original. For all but the "center" triangle, recursively repeat this process, until you reach an arbitrary base case (such as when triangle side length is less than 10). Myriad variations on the basic task are possible—both with respect to the style/design of the triangle and of the algorithm used. Three examples are provided below:

Beyond the lesson

Many coding applications favor recursion over iteration. For example, recursion is particularly well suited for navigating data collections structured as trees (as well as navigating maps, as students who tackle the MazeEscape activity will see). Recursion is also useful for divide-and-conquer algorithms, such as for searching and sorting arrays. However, these two topics largely fall outside the scope of this curriculum.

A valuable application of recursion that is readily accessible to students at this point involves the use of callbacks. Recall from the notes to the previous lesson that one of the most important uses of callbacks is for continuations—that is, a callback function called asynchronously, typically as the result of a system event such as when a file has been loaded, the computer mouse is clicked, or data entry is completed.

The lesson's coding snippet example provides an example of calling continuations in a recursive way. When the user user presses the return / enter key or clicks on the submit button after entering data, the continuation callback is executed. This function is executed asynchronously, in response to the system event.

In the Pencil Code environment, it is possible to accomplish the same result using iteration, as follows:

finished = false
while not finished
  await readstr 'Are we there yet?', defer ans
  finished = ans.toLowerCase()=="yes" 
write "Finally!"
write "I thought we'd never arrive!"

This iterative alternative may seem relatively straightforward, that is misleading. The use of a while loop here is only practical because Pencil Code incorporates Iced CoffeeScript's powerful await function into its library. Without the await block, we'd be very hard pressed to accomplished this result without resorting to recursion. Thus, we see that when continuations are involved, recursion is much better suited than iteration.

What can go wrong

Infinite Recursion and Stack Overflow

Recursion can be a powerful tool for solving complex problems, but it also requires careful implementation to avoid exhausting available system memory and/or for causing the browser to hang, any of which will cause your program to crash.

Recursive functions can cause a stack overflow if the recursion depth becomes too large. This occurs when there are too many function calls waiting to complete, exhausting the available memory allocated for the call stack. Pencil Code may report stack overflow with messages such as

Oops, the computer got confused. 
It says: "Maximum call stack size exceeded"

RangeError: Maximum call stack size exceeded

A common, and easily remedied, cause for stack overflow is infinite recursion. Infinite recursion occurs when there is no base case, or if the function's conditional logic is written in such a way that the base case is never reached. The following blatently deficient script yields a stack overflow error nearly instantaneously:

sumToN = (n) ->
  return n + sumToN(n-1)

sumToN(2)

The stack is not the only constraint on recursive programs. A second issue is that computations can take too long to be carried out, causing the browser to noticibly hang. In the Pencil Code environment, scripts that hang for more than about four seconds are interrupted, owing to a failsafe in the Pencil Code environment (designed to give students a chance to save their work, which otherwise would be lost if the script were interrupted by the browser itself).

The problem is that recursive algorithms, even ones that seem trivially short, can be exceedingly inefficient computationally. The following script used to compute the n-th value in the Fibonacci sequence (i.e., 1, 1, 2, 3, 5, 8, 13, ...) provides an excellent illustration:

fib = (n)->
  if n < 3  
    return 1
  else 
    return fib(n-1)  + fib(n-2)

The problem in this algorithm is that the number of recursive calls grows geometrically with n, not quite as quickly as branches in a binary tree, but still quite fast. For example, computation of the 5th Fibonacci value requires nine calls to the fib function (represented by the blue boxes in the diagram below).

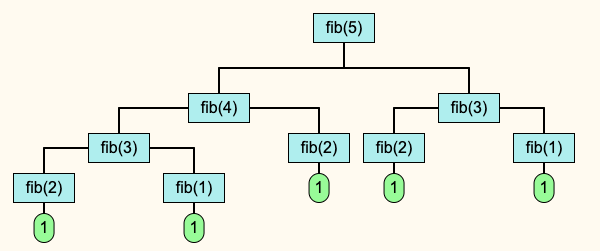
The computational efficiency of this algorithm is no problem for the first dozen or so fibonacci numbers, but soon the proliferation of function calls will overwhelm even the fasted of processors. Computation of the 33rd requires over 7 million recursive calls. My computer (a 2023 MacBook Pro, running Chrome) hangs before it can complete the computations for the 34th value in the sequence.

Oftentimes, an iterative solution may be an effective alternative to an inefficient recursive algorithm. It is certainly the case that iteration can be used to compute Fibonacci values in milliseconds.

However, that doesn't mean we must give up on recursion. It is often possible to refactor the code to make the recursion more efficient. For example, the following script relies on memoization for vastly improved performance when computing Fibonacci values. Memoization is a technique that involves storing the results of expensive function calls and returning the cached result when the same inputs occur again.

fib = (n)->
  return fibList(n).pop() # return last value in memo

fibList = (i)->
  calls++
  if i == 1
    return [1]
  if i==2
    return [1,1]
  sequence = fibList(i - 1)
  n = sequence.length
  sequence.push sequence[n-2] + sequence[n-1]
  return sequence

see fib(30)

Technicalities

In the JavaScript runtime environment, the call stack is the mechanism by which the JavaScript engine keeps track of function calls in a program. This is necessary because each time a function is called, JavaScript creates a new execution context, which contains information about the variables, functions, and objects that are currently available to the code being executed. (This is directly related to the issue of variable scope, discussed in depth in the notes to the Custom Functions! lesson.) The execution contexts in the program are tracked using a stack—the call stack. Every time a function is called, the new context needed for executing that function is pushed on the call stack. When a function completes, that context is then removed (popped) from the call stack, and the next-highest context becomes active.

As with any other function call, each recursive call generates a new copy context on stack memory. Once that function call completes, the context is discarded and memory is freed up. The challenge with recursion, however, is that it tends to rapidly swell the number of items on the stack. This presents a problem because of the physical limitations of the system: too many incomplete function calls exhaust the available memory. Situations in which the recursion depth becomes too large thereby cause a stack overflow error, causing the program to crash.