Teacher's Guide: Coordinates!

Overview

This lesson introduces a number of additional sprite movement functions. These functions open up a range of alternative algorithmic possibilities for solving coding challenges.

More about the lesson

The use of coordinates can make it much easier to move sprites to desired locations and thereby facilitates drawing more complicated shapes. Coordinates-based movement functions are fairly straigtforward to use, but using them effectively to solve coding challenges often takes quite a bit of practice. Their use requires a new way of thinking than was used when working solely with fd/bk and lt/rt. The differences between the functions are somewhat subtle; many students tend to initially underappreciate the distinction between absolute and relative movements.

In-class demonstrations using coordinates-based functions illustrates their usefulness and can highlight the distinctions between related functions (e.g., moveto versus movexy versus slide). For example, you might work as a class to construct triangles using absolute and relative coordinates, ultimately yielding something similar to this example.

Using triangles is a good choice for in-class examples not only because they involve only a few points, but also because it is a simple way to illustrate that the movement functions introduced in this lesson broaden the range of possible shapes they can draw without resorting to 'guess and check' and approximations. Previously, students were otherwise largely limited to equilateral triangles or perhaps a few familiar right triangles. But now they have infinite possibilities—a fact that holds for other shapes as well.

turnto accepts postive or negative angle arguments of any magnitude. Angles larger than 360 in abolute value are treated as the remainder of the angle divided by 360 (i.e., angle%360, as discussed in Mod and More!).

Being able to call jumpto 0,0 gives us a simpler alternative to home. The advantage of using jumpto 0,0 is that it does not have the additional side effects caused by home, most notably returning a sprite to its original orientation (facing "north"), but also undoing calls to grow, scale, mirror, and twist. A call to jumpto 0,0 therefore gives the coder greater control.

jumpto and moveto also provide students another method to move to random locations about the screen, such as with calls to

x = random([-300..300])
y = random([-300..300])
jumpto x, y

or more simply as a one-liner,

jumpto random([-300..300]), random([-300..300])

Students most likely previously tried to accomplish the goal of moving to a random position by first returning to the origin using home, in order to ensure that randomly selected locations did not end up off screen. Use of coordinates-based functions in this fashion obviates the need for that step. Slight variations of the preceding coding snippet could also be used to choose a random position in a specific region of the screen.

movexy is similar to slide (introduced in Images!), but the two should not be confused. Both move the sprites along the direction of the hypotenuse of a right triangle with legs determined by the arguments passed to the function. The difference between the two functions is that the arguments to slide specify movements with repect to the direction the sprite is currently facing, while the the arguments to movexy specify changes in the x-direction and the y-direction (always horizontally and vertically with respect to the screen).

Notes to activities

The activities are designed to encourage students to explore the differences between the different movement functions introduced in the lesson and compare and contrast the relative advantages of each in different situations. The first three activities are designed not just to get students working with each of the newly introduced functions, but also to get them thinking computationally

Some students will quickly transition to these new tools and the alternative approaches to solving problems that they yield, but others will likely struggle to get started. Provide scaffolding by encouraging them to code a square using specific coordinate values starting at the top left corner:

jumpto 100, 100
moveto 150, 100
moveto 150, 50
moveto 100, 50
moveto 100, 100

The key is getting students to recognize the underlying pattern of how the coordinates change. To generate an algorithm required of the full solution, remind them to think in terms of the turtle:

For the LightningBolt activity, students will likely have a more positive experience, and save time, if they begin by sketching their design on graph paper before turning to code. While moveto and jumpto can be used to draw an initial design, students who hope to succeed at the optional challenge will likely want to use slide. Finally, an optimal solution will allow scaling—i.e., use a variable to facilitate changing the scale of the design.

Additional activities

• RandomTriangle: draw a triangle based on three randomly chosen coordinates.
• The functions introduced in this chapter facilitate drawing triangles of any dimension. Unless you are familiar with right-triangle trigonometry, when drawing with fd/bk and lt/rt, you are limited to familiar triangles (e.g., equilateral, 30-60-90 or 45-45-90) or guess-and-check. Demonstrate your proficiency using the functions introduced in this chapter by drawing a SymmetricTriangle with randomly-chosen values for the base, height, location, and orientation. (The dashed line down the line of symmetry is optional.)
• Create an optical illusion by drawing a grid of lines on a solid background. Save your code as IllusoryDots.

• Coordinates functions can greatly simplify creating art. For example, consider this Pumpkin:

• Coming up with the list of coordinates or movements needed to instruct the turtle to draw a picture such as a Pumpkin can be challenging, especially for more complicated works of art. To simplify the process, it can help to draw a picture on paper first and then identify coordinates based on that. Create a GraphPaperArt script by using graph paper to help find a list of coordinates corresponding to a drawing of your own design. The following script illustrates the process:

• Connect lines from regularly-spaced points around a box, to create an 8-pointed BoxStar.

• Repeatedly draw lines from (0,200) to (x,0) to (0,-200), using ever-increasing values for x, to create a KinkyLines program. Make the program even more interesting by gradually changing the colors with each new kinky line.

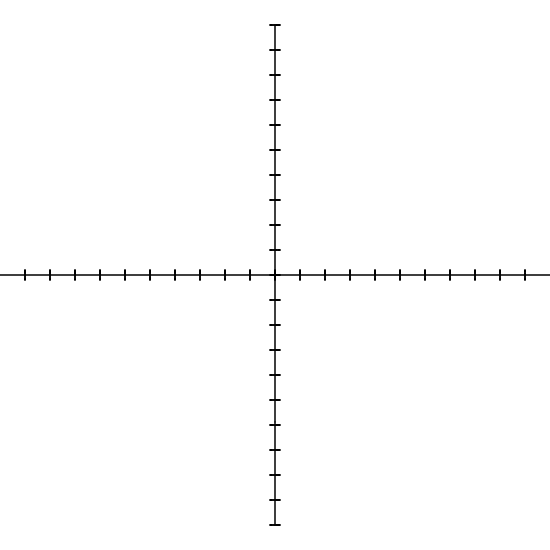
• ArraySquare: The movement functions introduced in this lesson also accept arrays as arguments. For example, moveto [100,50]. Repeat the AbsoluteSquare (or RelativeSquare or SliderSquare ) activity, but this time saving your coordinates (or movements) in an array. Because you will need to save each coordinate (or set of movements) as an array, your coordinates will be saved as an array of arrays, i.e., a nested array. Loop through your array of coordinates (or movements) to draw the square.
• Make a MathAxes program that shows the Cartesian Coordinate System, complete with tick marks. Then copy that code to a a separate PolyGraphs program add some familiar mathematical curves to it, such as y=x² or y=x³.
  

  Note: the PolyGraphs activity tends to be difficult primarily because of issues of scale. The challenge is that the scale that the students "see" on the screen (associated either with their MathAxes tick marks or each gridline on the background of the Pencil Code output pane) does not typically match the systems units (i.e., 25 units between each grid line). Encourage students to work this out, though working out the details exactly may prove a bit much. A good compromise may be, once they've identified the challenge, to simply apply an arbitrary scale factor, which need not match up with the tick marks they created for MathAxes.

Beyond the lesson

Test Console Widget

A useful, but oft-overlooked feature of the Pencil Code development environment is the measurement widget. Activate the tool by clicking the yellow box in the bottom right-hand corner of the screen, which normally shows current position of the mouse.

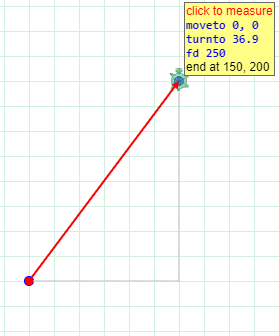
After activating the widget, click on a start point and then an end point. The widget provides the information needed for a turtle facing north in the start position to get to the end point, using either moveto or a combination of turnto and fd. The example below illustrates using the tool to compute an interior angle and the hypotenuse of a 3-4-5 triangle.

HTML coordinates

The Cartesian coordinate system used in the Pencil Code environment makes use of center-based values. Pencil Code also supports an alternative coordinate system, known as HTML Coordinates. HTML Coordinates position the origin in the top-left corner of the screen, with the positive x and y values extending to the right and downward. HTML Coordinates are saved in Pencil Code as Objects. For example, loc = {pageX:100,pageY:200}. HTML Coordinates will be introduced to students in a coding activity in the Custom(ized) Objects! lesson.

Array and object arguments

In this lesson, student learn to use turnto with a single argument that represents the bearing in which to point the sprite, and they learn to call moveto, jumpto, movexy, and jumpxy with pairs of numeric arguments. In subsequent lessons, students will learn to work with these functions with alternative arguments which represent coordinates on the screen. For example, jumpxy [0,0] relocates the sprite at the center of the screen, jumpxy {pageX:0,pageY:0} repositions the sprite in the upper left corner; and turnto [0,0] points the sprite to the origin. Additionally, moveto, jumpto, and turnto also accept other objects that can be resolved to locations as arguments, such as sprites—the focus of the upcoming lesson Chase Other Sprites!.

What can go wrong

moveto vs. moveTo

The Pencil Code function names in this lesson don't follow the camel case convention. Having developed good habits, students may mistakenly enter some of these functions using camel case, in which case they will run into errors. In most cases, such as trying to execute jumpTo 0,0, mistyping the function name will have the same effect as mistyping any function or variable name: the program will crash because the variable name is not recognized. Formally, this is an example of a ReferenceError.

However, the statement moveTo 0,0 will not result in an error being reported, and in fact nothing will appear to happen. The reason is that moveTo is the name of a built-in Javascript function designed to minipulate the web browser window (for an example, see w3schools.com), though it tends not to have any effect if called in the context of a Pencil Code sprite. Given this lack of system feedback, this type of error can be particularly perplexing. The upshot is that we can't be overly reliant on error reports for debugging, we have to keep program behavior in mind.

Pedagogy

Chosing the hard way: the example of random(position)

The statement jumpto random(position) provides a convenient means by which to position a sprite randomly in the visible window. This approach to moving a sprite to a random position has the additional advantage of selecting coordinates based on the underlying dimensions of the visible screen, rather than using hardcoded values that students base on browser-specific settings. But despite these benefits, however, this curriculum has intentionally avoided introducing jumpto random(position) thus far in the curriculum, and recommmends continuing to discourage its use for several more lessons.

Part of argument against student use of jumpto random(position) is tied to technical factors. Prior to this lesson, students hadn't yet learned about functions such as jumpto and moveto, so they lacked a key ingredient of the expression. But even now, students aren't really equipped with the background to fully understand the function call random(position), because it returns an object representing HTML coordinates—two concepts with which students are as yet unfamiliar.

This curriculum recommends continuing to eschew use of random(position), but based less on these technical justifications, but for the simple though somewhat ironic reason that the expression is too convenient and too easy. Allowing students to rely on calls to jumpto random(position) deprives them of the important opportunity to work out algorithms on their own, and to explore variations of those algorithms. Letting them take the "easy way" would undermine the goal of developing computational thinking skills.

If students had immediately relied on jumpto random(position), they would have missed out on the opportunity to experiment with, and to explore the relative strengths and limitations of, different algorithms for choosing random positions. For example, an algorithm students likely worked up early in this curriculum is to instruct the turtle to make a random turn and then move forward a random distance. Many students by now likely have recognized, perhaps with teacher prompting, that this algorithm suffers from a number of shortcomings, not least of which is that it results in locations that are more densely populated around the origin then they are further out. This may motivate them to work up an alternative algorithm, such as: moving forward a (perhaps negative) random distance, turning 90 degrees, then moving forward again. This algorithm provides a more uniform distribution of outcomes. With slide as well as the functions introduced in this lesson, students can come up with more succinct variations on this theme, particularly when combined with array inputs, e.g.,

slide random([-100..100]), random([-100..100])

Given the limitations they faced earlier in the curriculum, students will more greatly appreciate the advantages afforded by the functions introduced in this lesson. From all this, students will gain a more nuance understanding of the process of choosing a random location and the tradeoffs of different approaches. An early introduction to the useful expression jumpto random(position) undercuts this learning process. In summary, doing things the hard way is more beneficial for student learning. This is why it continues to be better not to introduce jumpto random(location): it undermines this devepmental approach.