Teacher's Guide: Math, Mod, and More!

Overview

This lesson provides students with additional mathematical tools regularly used in advanced coding and computational problem solving. This lesson is a bit more "mathy" than others, but that is necessary to provide exposure to these important tools used by programmers.

More about the lesson

The operators and functions introduced in this section are generally straightforward, so that students have little difficulty understanding them. The challenging aspect to the features introduced in this lesson are applying them effectively in solving computing challenges. As a result, these teacher notes will focus disproportionately on notes to the activities.

The lesson points out that many Math functions can be referenced in Pencil Code without the prefix Math. Pencil Code makes Math properties available as global variables, making it unnecessary to enter the Math object name. Thus, PI works the same as Math.PI. This explains why students have been able to use random all this time, without specifying its full reference Math.random.

Students will probably not be surprised to learn that there are often multiple ways to carry out any given mathematical operation. For example, consider the case of integer division. 20//3 is equivalent to floor(20/3). In theory there could be slight performance advantages to one approach or the other, but these are so small as to be of no concern to coders at this level.

String interpolation may seem like an out-of-place topic for this unit, but it actually makes sense when you consider it's relationship to the + operator. The + operator can be used to join strings. When used this way, + is called the concatenation operator. String interpolation offers an alternative to concatenation, allowing one to build up strings with embedded expressions without lots of quotes and plus signs.

A benefit of string interpolation is that it helps students avoid errors involving order of operations. For example, given two number values defined as x = 5 and y = 7, the expression "sum = #{x+y}" yields the (presumably) intended sum in the string, "sum = 12", but "sum = " + x + y would yield the purely concatenated variant sum = 57. The reason for this is that the order of operations is from left to right. Javascript processes each number individually, coercing it to a string and concatenating it with the string on the left as it parses the expression. As usual with "PEMDAS" situations, adding parentheses is also an effective means to achieve the desired result: "sum = " + (x + y)

Notes to activities

BrokenMath: Miscalculations when working with fractional values arise because computers perform computations in binary (base 2), rather than in decimal (base 10). The issue is that some numbers that in base 10 can be expressed exactly using a fixed amount of storage can only be approximated using a fixed number of digits in base 2. For example, in base 2, the decimal value "one tenth" (0.1) results in abinary repeating fraction, 0.000110011001100.... Given a fixed number of digits used to store numeric values, this value gets rounded, resulting in a value not exactly equal to one tenth. When these rounded base 2 values are summed, the rounding errors can accumulate sufficiently to lead to notable computation errors in decimal values, even for seemingly simple math problems.

Because the resulting rounding errors are very small (in the case of the sum of three tenths, the error is 0.00000000000000004) a conceptually simple workaround is to round the number to a smaller number of digits. However, Math.round always rounds to the nearest integer, so the job is a little more involved in practice. To round the number x to four places (not necessarily four places to the right of the decimal point), use Math.round(x*1000)/1000.

The Countdown activity involves significant computational work. Encourage students to focus first on the computations, putting off formatting until later. Students would be well-advised to revisit the Date Objects! lesson to refresh their memories of key features of the Date class, such as that new Date() yields the current date and time and the fact that the month value in the Date constructor is 0-based, i.e., new Date(2000,1,15) represents midnight on February 15, 2000. Perhaps most importantly, for the sake of keeping this proejct (relatively) simple: remind students that subtracting one Date from another yields a difference in milliseconds.

Given the ease with which we can compute the number of milliseconds between two dates, the primary challenge in this exercise then becomes converting that difference into larger time units, i.e, number of days, hours, and so on. (Younger students, particularly those who have not yet taken Algebra 2, may need some additional general help to get started, as they may be less familiar with the idea of the logic of unit conversions.)

One approach to the computations necessary for this activity is to use integer division and modulus operators, starting with the number of days. Given millisecondsPerDay = 1000*60*60*24, comput the number of days as follows; then in subsequent code, use the remainder in an analagous fashion to compute hours, minutes, and seconds:

An alternative to the foregoing algorithm is employed in the following alternative birthday countdown (see the source code for details):

Students should work with fixed Date values until they have successfully worked out the math of unit conversions. The iteration required to keep the computation current (showing changing seconds and minutes) should be saved for last, even after formatting, potentially best viewed as an optional extension.

Checkerboard: This activity is included in this lesson because students need to compute an integer number of blocks (i.e., there should be no partial blocks). It is possible to address this challenge using comparison operators, but the mod operator is more appropriate. The other main challenge in this activity is deriving an algorithm to alternate the color of the blocks from row to row and from column to column. This aspect of the activity is a good application of conditional logic.

Additional activities

• DigitalClock: Using only formatted labels, create a functioning digital clock that shows each digit separately. That is, you should have 5 labels: one for the body of the clock, and one each for the ones digit of the minutes, the tens digit of the minutes, the ones digit of the hour, and the tens digit of the hour. Obtain the system time using a Date object, and from this obtain values for hours and minutes using the getHours and getMinutes methods. As an added challenge, keep this clock running using iteration, updating the values of the labels using the jQuery selector methods discussed in the Label Recycling! lesson.



• RandomChallenge: We have always used random with an argument, i.e., random(100), random(color), random([1..100]). However, are there other possiblities? In fact, yes. One is to use two arguments, showing the min and max (well, one more than the max), i.e., random(1, 101). You can also use random without an arg, i.e., x = random(), which yields a number 0≤x<1.

  For this activity, pretend that the only way to generate a random integer was to start with this no-args version. How would you generate the equivalent of random(100) or random(1,101), using only calls to random() (with no arguments)?

  Hints: start trying to match something more simple, such as random(4) (which yields values 0,1,2,3). Then move on to random(0,4), and finally random(-3,4) (for values -3 through 3). A variety of solutions is provided in the example program. If using Math.round, pay particular attention to endpoints, including that minimum and maximum values are equally likely to get selected. (Math.round(random()*4) can yield 5 values (0 through 4), but the lowest and highest are only half as likely to occur. Math.round(random()*4 - 0.5), on the other hand, yields only values 0 through 3, with equal likelihood of selection.

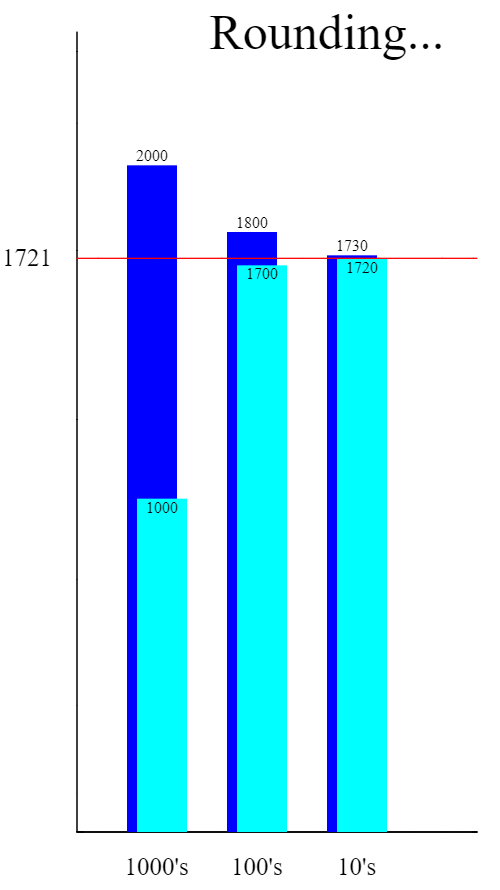• RoundUpOrDown: The round function automatically rounds to the nearest integer, a.k.a. the nearest ones digit. However, sometimes we will want to round to some other digit, such as the tens or hundreds (to the left of the decimal point), or the tenths or hundredths (to the right of the decimal point). Additionally, sometimes we want to intentionally round up or round down, regardless of what generic rounding would do. In this activity, generate a random integer with up to 4 digits. Compute this number rounded up and rounded down, to the nearest thousands, hundreds, and tens. Compare the different values graphically.
• Prime numbers are whole numbers greater than one that are divisible only by themselves and 1. They are integral to the encryption algorithms used to make internet communications secure, and also in some formulas to generate pseudo-random numbers. Write a program called IsPrime that determines if a randomly generated number, n, is prime. An effective strategy is to begin by assuming that n is prime, and look for evidence that it is not—specifically, a number that evenly divides n. If n%i==0 for some number i between (but not including) 1 and n, then n is divisble by i and therefore n is not prime. You can only conclude that n is in fact prime, as originally assumed, if you have checked all relevant values of i and haven't come across one that satisfies n%i==0.

Beyond the lesson

Additional Math methods

This lesson introduces a number of tools in the Math class, but there are many more. For example, Pencil Code provides two versions of each trig function (e.g., sin and sind, for radian and degree arguments, respectively), logarithm functions for different bases (log(x, base)), and so forth. A thorough online reference is MDN web docs.

Static versus non-static methods

The examples of object methods described thus far have nearly all functioned with respect to a specific instance of an object. For example, the fd function can only be called on a specific Turtle instance. However, methods can be defined based on a particular object type itself. Such methods are called static methods.

The various Math class methods we use are static methods. Another example is the Date object's now method. Rather than construct a Date object to get a timestamp (by calling new Date(), such as we did for the ProgramTimer activity in the Date Objects! lesson) one can use the Date class's now method to generate the number of milliseconds since midnight on 1/1/1970. Hence, beginTime = Date.now() is equivalent to

d = new Date()
beginTime = d.getTime()

Useful methods of the Number class

As noted in the Notes to the Date Objects! lesson, the Number object is a wrapper class provided by JavaScript to facilitate working with numbers. This wrapper class effectively adds methods to numbers, even though numbers are not objects, and therefor can't have methods. (Refer back to those earlier notes for details). Two methods of this class relevant to this lesson is are toFixed and toPrecision.

The toFixed method converts a number to a string variant that only has two digits to the right of the decimal point, rounding if necessary. For example, suppose that x references the number 1234.5678. Then x.toFixed(2) will return the string "1234.57".

The toPrecision method generates a string representation of the value with exactly four digits (also rounding when appropriate). For example, suppose again that x references the number 1234.5678. Then x.toPrecision(4) produces the string "1235". When number values have a greater number of digits to the left of the decimal point (i.e., radix) then the argument passed to toPrecision, then the method returns a scientific-notation representation of the value. For example, 12345678.toPrecision(4) returns the string "1.235e+7".

What can go wrong

Line Number warning () w.r.t. the // operator

You can safely disregard the warning flag that appears to the left of the line number containing the // operator.

String interpolation fails

String interpolation requires the use of double quotes. A string constructed with single quotes will be remain in its literal form. Thus, if x references 5, "The value of x is #{x}" evaluates to the string "The value of x is 5", but 'The value of x is #{x}' stays in its literal form.

Exponentiation fails

Exponentiation can be carried out with the exponentiation operator, **, or the Math function Math.pow. However, given the use of ^ for exponention in other contexts, students might use it for that purpose here. Doing so will not yield an error, because ^, is a valid math operator. However, it will produce confusing results. ^ is one of a number of bitwise operators that compares binary representations of values based on individual bits. (Working with bitwise operators requires an advanced understanding of binary; this topic is outside the scope of this curriculum.)

NaN returned from min or max

The min or max functions only accept comma-separated lists of values. Attempting to pass an array will return the value NaN.

The Coffeescript splat operator, ..., provides an easy solution. Recall that, when appended to an array in a context where a list of values is expected, the splat passes the elements of the array to the function as if they were a comma-separate list of values. Thus, for example, max([1,4,2,5,6,3,2]...) will return 6.

Technicalities

string interpolation versus template literals

String interpolation is a CoffeeScript feature, though it is very similar to (and in fact, as of CoffeeScript verison 2, compiles to) the JavaScript feature template literals.

The template literals syntax used in Javascript differs from the syntax used in Coffeescript. As noted above, Coffeescript literals are created using double quotes and a hash tag, e.g., "This sum is #{x}". In Javascript, the syntax uses a backtick (a.k.a. grave accent) character and dollar sign: `The total is ${x}`.