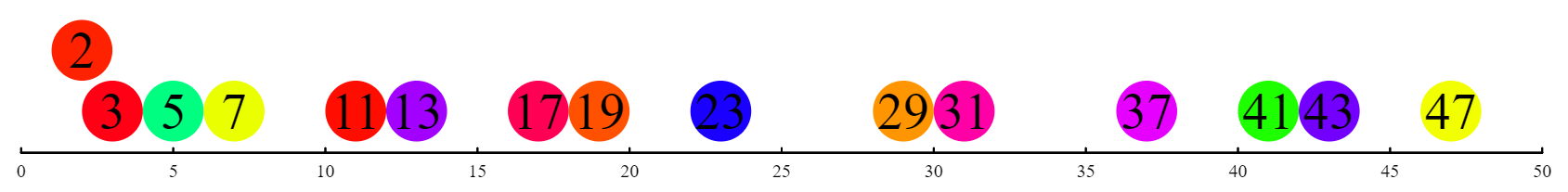Teacher's Guide: Logic Operators

Overview

This lesson provides an introduction to the use of logic operators, powerful tools for concisely expressing more complicated conditional logic. This lesson introduces the three Boolean operators, and, or, and not. The goal is to expose students to an alternative to constructing complicated conditional logic structures involving nested if/else statements. It also provides students additional opportunity to work with the broader underlying topic of conditional logic.

Note that this lesson does not provide a thorough introduction to Boolean logic. For example, it does not explore properties of the operators when used on combination (e.g., commutative, associative, and distributive properties, or DeMorgan's laws). Nor does it formally introduce related concepts and tools, such as Venn diagrams or truth tables (though teachers may find it useful to broach such concepts, depending on their particular situation). The emphasis is on relatively simple, practical applications, and not on broader theoretic properties and nuances.

More about the lesson

As a lead-in to this lesson, it may be useful to remind students that every Boolean expression evaluates to true or false. A simple Boolean expression might look like turtle.touches(green) or x==5. This lesson is about writing code to express more complicated boolean expressions.

The basic concepts of boolean logic are straightforward and already familiar to students. The challenge is applying these concepts to more complicated, compound expressions; though, admittedly, this lesson does not press students to extend to far down that path. Rather, it challenges students to construct fairly straightforward compound expressions, such as determining if a single value simultaneously satisfies multiple criteria, e.g.,

x>-100 and x<100 and y>-100 and y<100

The goal is basic familiarity with these operators. Students will surely develop greater expertise over time, with practice and potentially further study of Boolean logic.

Note that we don't really need the Boolean operators introduced in this section, because we can get the same results using nested if statements and comparison operators. For example, not(inside(window)) is equivalent to inside(window)==false. However, Boolean operators can make our code more succint and also more readable. For example, simultaneously testing values of x and y, as was done in the one-liner above, would require several nested if statements:

if x>-100
  if x<100
    if y>-100
      if y<100
        #more code

Used in conjunction with variables, boolean operators can be especially useful testing compound conditions in while loops. The following functionally equivalent snippets illustrate the potential savings in code:

incomplete = true
while incomplete
  # more code...

  if distance(0,0)>100
    if touches(green)
      incomplete = false

Versus this much more parsimonious solution, which also places the logic at the top of the loop, making it easier to read:

while distance(0,0)>100 and touches(green)
  # more code...

Notes to activities

The use of logic operators is a minor but important part of the SnakeEyes script. Drawing on prior knowledge, students ideally will opt for a while loop. The loop should continue as long as both dice rolled are not equal to one. Students may come up with something like the boolean expression (roll1==1 and roll2==1) == false. Arguably a more elegant solution is not(roll1==1 and roll2==1). With respect to dice images, students can create their own (recall the DieMaker activity in the Notes to the Arrays! lesson), or identify relevant images on the web.

Depending on how they tackle the WhichQuad activity, students may find that the colored quadrant flickers. However, don't let them settle for that. "Fix-ups" might include using additional conditional logic, such as to only redraw that quadrant when the turtle enters the space (this is the approach taken by the illustrated solution). In this case, students would need to use a boolean variable to track whether the turtle has already entered that region. Alternatively, they can create appropriately-sized colored sprites for each quadrant, and call show when the turtle is in that space. Given that subsequent calls to show would have no effect if the sprite is already visible, there would be no flicker.

The Predator activity is ambitious, but manageable for all students if they approach the challenge step by step. As always, coach them to decompose the task into smaller parts, focusing on one aspect at a time. For example, one might first code the movement of the "prey." Then add in the movements of the predator—which will involve animation queue considerations, to keep the turle in sync with the prey.

The illustrated solution for Predator uses speed Inifinity and also a while loop, with the sprites making small movements each turn to get the right look. Use of speed Infinity has the dual benefit of making motion smoother and obviating the need to make multiple calls to await done defer() (e.g., for the touches function). However, given this setup, it is necessary to embed at least one call to await done defer(), as a trick to avoid excessively long queues from stacking up (and causing the program to crash).

Additional activities

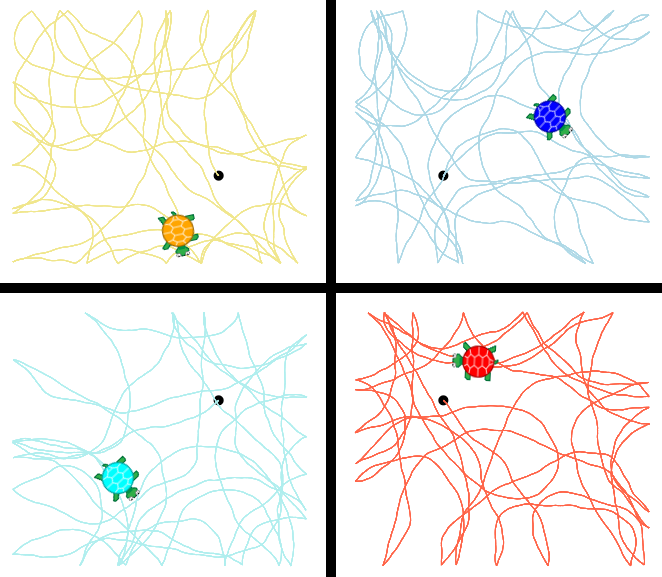
• Divide the screen into quarters, and put a randomly moving turtle into each of the FourCorners. Without using touches or inside, keep each turtle in its own corner.


(Teacher's note: Encourage students to decompose this problem, to make solving it easier. Specifically, you might suggest that they work with one turtle in one corner, and figure out the logic to keep that turtle contained there. Then it is fairly straightforward to replicate by copying that solution and making the necessary modifications.)

• There are many algorithms for finding prime numbers. One approach (first suggested in the Notes to the Math, Mod, and More! lesson) is to check if a possible prime (call it n) is divisible by any of the numbers less than it (excluding one)—if not, then n is prime. However, a much more efficient algorithm would only check these possible factors that are less than half as big as n (why?). Write a script that searches for prime numbers, using this more efficient algorithm that checks two conditions, i.e., whether the possible factor is less than half of the potential prime and whether the potential prime is divisible by the possible factor. After you have succeeded at coding an algorithm for testing if a given number is prime, incorporate it into a loop that looks for a broader set of primes: either the first 100 prime numbers (naming your program FirstNPrimes) or all primes less than 100 (naming your program PrimesUpToN). Output your findings to the screen using label. (Get creative, as illustrated in below!)
  
  
  
  
  

  BTW: there are much more efficient algorithms for finding primes. Can you think of ways to improve your algorithm? A simple way to measure the efficiency improvement of your algorithm is to use your ProgramTimer code from the Date Objects! lesson.

Beyond the lesson

Order of operations

Boolean expressions follow a set of rules regarding order of operations (i.e., akin to "PEMDAS" in math class), not only with respect to other boolean operators, but also with respect to other operators, such as multiplication or addition. When considering these operators only within the context of other boolean operators, and evaluates before or, and not comes before both of them. Thus, for Boolean values A and B, the expression not A and B is equivalent to (not A) and B.

Things can quickly get more complicated when combining boolean operators in expressions containing other operators, such as arithmetic operatiors (e.g., + and ×). The Boolean operators and and or have very low precedence, so they will evaluate after mathematics are carried out. However, not is evaluated before arithmetic operators. This owes to the fact that not is a unary operator, meaning it acts on only one input. (Other unary operators students may have encountered thus far include -- and ++, e.g., x++). All unary operators take precedence over binary operators.

As an example of how challenging it can be to work out how order of operations apply to Boolean expressions, consider the expressions not(9==10) and not 9==10. The former evaluates to true; but perhaps surprisingly, the latter evaluates to false. Owing to order of operations, not 9==10 is evaluated as (not 9)==10, which simplifies to false==10. This is a valid expression which evaluates to false owing to the truthy-falsy nature of boolean expressions in Javascript (see the discussion on type coercion in the Notes to the Comparison Operators! lesson).

Properties of boolean operators

Boolean operators also have special rules relating to associativity, transitivity, and distributivity, in particular when mixing operators. For example, not(A and B) is equivalent to (not A) or (not B) (this is an example of one of DeMorgan's Laws; the other is that not(A or B) is equivalent to (not A) and (not B) ). These rules are fairly straightforward to demonstrate using Venn Diagrams, though they are not intuitive and therefore take a good deal of time to master, and are anyhow too theoretical for most applications in this curriculum.

As noted above, students are encouraged to use the operators in straightforward ways where it can help improve the simplicity or readability of their code. If they stick to fairly straightforward logic statements and make heavy use of parentheses to ensure expressions are evaluated as desired, they should not run into too much trouble. For more complicated expressions, a mix of logic operators and conditional logic statements may be the safest solution.

Compound inequalities

Coffeescript allows for compound inequalities, such as 100>x>-100. However, this feature is not broadly supported in other languages, so it is not introduced to students here. Rather, students should code such expressions using boolean operators, i.e., 100>x and x>-100.

Venn diagrams and truth tables

Venn diagrams are used to provide a graphical interpretation of expressions involving logic operators. Students may already be familiar with this tool from other coursework. Truth Tables effectively do the same thing, using a tabular approach (as illustrated below). Both of these tools can be useful for making sense of logic expressions.

Javascript logic operators

The CoffeeScript operators and, or, and not are equivalent to the Javascript equivalents &&, ||, and !. The Javascript operators can be used interchangeably with the CoffeeScript operators.

What can go wrong

Logic errors

Invariably in a lesson using logic operators, students will make misspecifications that cause their programs to fail to run as desired. These errors can be especially hard to debug in programs involving random values, as the code may work intermittently. A great first approach is to try to work out the desired logic on paper, such as using tree diagrams or Venn diagrams. Additionally, general debugging practices can be very useful too. For example, students can add statements to output information to the console which they can use to analyze where and when their program is failing.

Omitted parentheses

As students have surely encountered by now, CoffeeScript's flexibility on omitting parentheses sometimes leads to undesired results. This holds for logic operators as well. It is sometimes necessary to add parentheses to statements involving logic operators to ensure that the code gets parsed the way you intend. As an example, consider the following code

while not turtle.touches green and moves<20

This results in a runtime error and the following rather cryptic error message (which actually relates to the touches function):

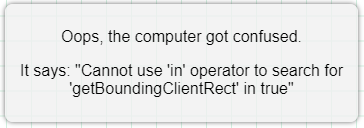
A look at the same code in block form provides insights into what has gone wrong:

A quick read of this code reveals that CoffeeScript has not parsed the code as was intended. When the code is evaluated, CoffeeScript applies truthy-falsy rules to evaluate green and moves<20 (which is false), and then passes that result to touches. touches throws an exception, because it cannot accept a Boolean argument.

Adding parentheses, we can force CoffeeScript to parse the expression as intended:

The upshot is that it is a good practice to include parentheses when using boolean operators, especially in compound expressions. This not only helps ensure that there is no mixup in the order of operations, but also contributes to better readability.

Mixing up assignment and comparison

As noted in previous lessons, mistaken use of = in place of == leads to confusing situations, because of the truthy-falsy nature of Javascript. if (distance=20) not only sets distance to 20, but behaves like if true.