Teacher's Guide: Curved Line Art!

Overview

This lesson has two main goals. First, it introduces the two-argument variants of the rt and lt functions, the only built-in Pencil Code functions that draw curves. Second, the lesson formally addresses the concept of algorithms and thinking algorithmically.

More about the lesson

The rt and lt blocks are the same ones as students used in previous lessons. This time, however, students will make use of the optional second argument, specifying the radius of an arc.

A useful analogy for introducing the call to the rt and lt functions with two arguments is pivoting in basketball. When a basketball player pivots, he or she "plants" one foot and spins around on it, with the other foot swinging around. The foot in motion traces out an arc with radius equal to the distance between the two feet.

An important takeway from this lesson is that everything that appears on our computer screen is an illusion. For example, there is no actual motion. Just as when watching a movie, what you see is just the illusion of motion caused by tiny lights turning off and up to 60 times per second (on a typical 60 hertz monitor). With respect to artwork involving curves, students will use "chunks" of circles to give the illusion of curves that are not circular in nature.

In designing algorithms, we can harness the power of math (such as when we capitalized on the relationship between turn angles and number of sides in polygons), and other patterns and relationships as well. Symmetry is one such example. Using symmetry can nearly cut our work in half.

Notes to activities

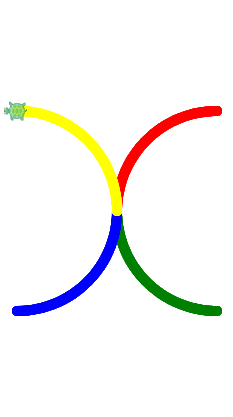
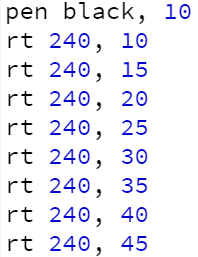
The activities are designed not only to give students much-needed practice with drawing curves, but also to promote problem solving and algorithmic thinking. Though the solution is simple, the Spiral activity tends to be a difficult one for students to get started with, which is why the instructions include a big hint (to start by drawing consecutive half-circles). Ideally, students will explore different variations, based on modifying the radius and/or the turn angle in different ways. There are many ways to get the "hand drawn" effect, including mixing up the angles and/or different arcs rather than following a consistent pattern. However, more complicated is not necessarily "better." The example solution on this sheet simply uses arcs of 240 degrees that have radii that grow at a constant rate:

The ROYGBIV and OlympicRings can likewise be coded using a variety of algorithms, a point to explore with students after they have come up with an individual solutions. For example, consider the four alternatives to ROYGBIV illustrated in the following (clickable) examples:

Yet another way to approach this activity—though one that does not support "curved line art"—is to draw concentric circles, and then remove the bottom half, either by overwriting it with a horizon or a color that matches the background (or perhaps even erasing it, by drawing over it with color erase).

For the fish activity, it can be useful to capitalize on symmetry. For example, first draw the top half, including using fill, then either backtrack or use home to return to the starting point and draw a mirror image. Using this strategy, it is not essential that the top "half" is exactly one half of the image—someoverlap is ok, as illustrated in the following example that illustrates coding a heart:

Additionally, a good strategy is to start with a simple outline of the body, then add to that, layering in things like eyes, gills, fins, stripes or other features.

Additional activities

• It is possible to have symmetry about a line and/or about a point, as illustrated in the following examples:


Yet another form of symmetry is rotational symmetry, when a pattern is repeated around a central point. Code a script that draws a Flower using rotational symmetry.


• Design a Rocket with curvy sides, such as the Pencil Code Rocket.


• Code Eyes...
  

  ...or time permitting, perhaps an entire Face!

  
• How about a RecycleSymbol? Or a Baseball?

Beyond the lesson

show and hide

Because they are functions that do not take an argument, show and hide, like pu and pd, both require parentheses after them when calling them.

show and hide have aliases, st and ht, respectively, short for "show turtle" and "hide turtle". An alternative to show and hide is the toggle function, which changes the show/hide status of the turtle.

This lesson includes show and hide primarily for aesthetic purposes, i.e., hiding the turtle when we don't want to see it in our finished drawing. However, an important side effect of hiding a turtle is that it causes the pen animation to go away. While not a particularly important behavior now, when we get into iteration (and quickly code programs with many more function calls), this side effect can greatly speed up programs. For example, in the Colors! lesson, we may iterate hundreds of time, with a new pen color each iteration. Eliminating the pen animation can dramatically boost performance.

fadeIn and fadeOut

These alternatives to show and hide provide a less abrupt transition between visible and hidden. Control the duration of the fading animation by passing a numerical argument specifying time in milliseconds, e.g., fadeOut(2000).

These functions are not listed in the coding blocks palette, so they must be typed, with appropriate attention to their CamelCase spelling—calls to fadeout or fadein will prompt the warning "fadeout is not defined" and the program will crash.

Negative arguments to rt and lt

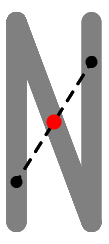
The rt and lt functions accept negative values for both angle and radius. Because the behaviors are not entirely intuitive, it is likely therefore best to discourage student use of this feature at this point. However, use of negatives in turn functions can be useful at times to more experienced coders. Rather than fully work through the logic in these notes, an example illustrating the four possible configurations of positive and negative arguments for each function is presented below. Another valuable resource is this interactive tool, which illustrates of the effects of modifying the two arguments.

arrow

The arrow function creates an arrow extending from the turtle’s current location, by a specified number of units. It syntax is arrow color, length (e.g., arrow red, 100). The line thickness is determined by the current pen setting.