Teacher's Guide: Custom Functions!

Overview

An understanding of functions, especially the ability to define custom functions, is a prerequisite for accessing the more advanced features of JavaScript. Custom functions allow students to harness interactive features of the web-programming environment, such as keyboard input and mouse clicks, as well as dynamic tools such as loading data or importing additional code from libraries. Functions are also integral to many other JavaScript features, such as class definitions and closures

This lesson commences the study of custom functions with an introduction to the syntax of defining functions and the use of functions for organizing code, facilitating code reuse, simplifying code maintenance, and improving program readability. It serves as a foundation for subsequent lessons that explore different aspects of this extensive and nuanced topic.

This set of teachers notes runs longer than most. This owes to the fact that the introduction of functions has the potential to open up a pandora's box of coding complications. Though the lesson is designed to keep things simple and focused, questions that deviate from this narrow path are almost certain to arise. These notes are provided in the hope that the informed teacher can fill in the gaps and provide student guidance as needed.

More about the lesson

Custom function syntax and use

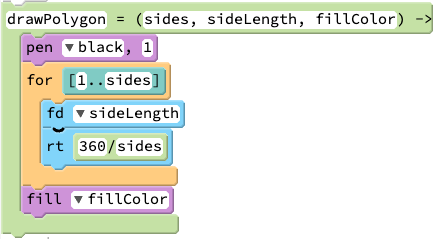
The fundamental concept of a function is straightforward: in programming, a function (also known, historically, as a procedure or a subroutine) is a sequence of instructions to be run as a unit. The CoffeeScript syntax for defining functions is straightforward and intuitive. Students can find a prebuilt block in the coding palette under Operators:

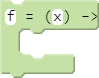
When no argument is specified, CoffeeScript allows us to omit the parentheses in the function declaration. For example, the following two snippets are equivalent:

Though conceptually simple, the use of functions opens up a range of complexities and with them a number of coding pitfalls. To avoid overwhelming students and to keep them focused on its primary objectives, this lesson limits the use of custom functions to tasks that involve directing the default turtle to carry out a sequence of steps, such as to draw a shape. For example, the following drawTriangle function encapsulates the code needed to instruct the default turtle to draw an equilateral triangle, starting in its current position, with side length and color determined by the arguments sideLength and color:

Once a custom function has been defined, it can be run with a simple function call, just like any built-in function. For functions that are called with arguments, parentheses are optional. Thus, for example, one can invoke the drawTriangle function with either of the following two statements:

drawTriangle(50, red)
        
drawTriangle 50, red

As always, functions that take no arguments must be called using parentheses.

When defining custom functions, it is good style to choose names that describe what the function does. Oftentimes, a suitable name comes in the form of an action phrase, such as drawCenteredSquare. The choice of variable name involves a tradeoff between clarity and succinctness. The name drawCenteredSquare has the benefit of being self-documenting, that is, one can infer what the function does based solely on its name. Variable names that are self-documenting benefit the readability of the broader program.

Benefits to using functions

The lesson's use of functions may lead students to mistakenly believe that functions are primarily useful as a convenience. Point out that this lesson is just the beginning of their study of functions, and that they will encounter additional, powerful applications of functions in subsequent lessons. However, as developing coders, it is important that they do not undervalue the benefits of functions that this lesson and its associated activities are designed to emphasize.

For starters, functions are a convenient way to facilitate code reuse. Reuse does not just reduce the number of lines of code, but it also facilitates code maintenance. Without functions, if a block of code is repeated at different points in a program, any edits to that block must be made to each of the copies of that block as well. This not only increases the time required for making modifications, but also opens up additional opportunities to make mistakes, either through typos or by failing to catch all the relevant parts of the program that need to be updated. In contrast, by using functions, such modifications would only have to be made once, in the function definition.

Functions' code-reuse benefit can extend beyond individual programs through code libraries. In short, programs can import (i.e., read in) functions that are defined in files saved elsewhere on the server or even on a remote site. In fact, this is how Pencil Code works. Most of the non-native functions (those not defined in JavaScript) used in this curriculum are either pulled directly from, or based on, functions defined in the widely-distributed jQuery library. Students will learn to make use of public libraries and also their own locally-defined libraries in a subsequent lesson.

Using functions also improves the readability of programs. A single function not only can replace many lines of code, but—if it well-named, in a self-documenting way that describes what it does, as suggested above—it typically also obviates the need even for explanatory comments. The single line of code drawCenteredSquare(100) not only instructs the turtle to draw the desired shape, but it succintly describes what the many lines of code invoked through that function call do. This saves someone reading the program from having to mentally parse the multiple lines of code contained in the function and facilitates thinking about the program at a higher conceptual level.

Admittedly, the custom function examples provided thus far in this lesson have been simple. All else the same, the benefits of functions are greater when the code they contain is more complicated and/or extensive.

Function arguments

Students have made regular use of function arguments from the very first lesson of this curriculum. Arguments provide a mechanism to explicitly pass information to that function, allowing the function to be used for a wider variety of purposes, a feature known as generalization. The greater the generalization of a function, the greater the potential for code reuse.

The following example illustrates of the benefits of greater generalization facilitated through the use of function arguments. The drawTriangle function, on the left, is easily modified to create the more general drawPolygon function, on the right. All it takes is adding another argument for sides, and replacing the fixed integers, 3, with references to that argument:

Admittedly, attempts at generalization can lead to significant algorithmic complexity. Generalization isn't always practical or feasible, but it is something to look for, as it is a powerful coding concept.

In the preceding examples as well as in the lesson, the only values passed as function arguments have been primitive values. Be sure that students don't overlook the fact that objects, including sprites, can be passed via arguments just like any other value. Aside from the issue of improved style associated with explicitly passing information to a function through its arguments, this also has the potential of offering a function with greater generalization. For example, the following variation of the drawTriangle function adds a third variable that explicitly specifies the sprite that will do the drawing, allowing for greater flexibility in how the function is used. This approach is clearly superior to writing a separate version of the function for each sprite.

drawTriangle = (sideLength, fillColor, sprite) ->
  sprite.pen black, 1
  for [1..3]
    sprite.fd sideLength
    sprite.rt 360/3
    sprite.fill fillColor

for i in [1..10]
  c = random color
  t = new Turtle(c).turnto(36*i)
  drawTriangle(100+random(100),c,t)

Scope

Scope is a topic of considerable importance in JavaScript programming. It can significantly impact how a script behaves when run, and also gives rise to powerful coding idioms. However, the concept is abstract, and the rules of scope are nuanced and can be hard to fully understand or appreciate until one has much greater experience writing custom functions.

In simplest terms, scope is a language feature that determines when and where variables are accessible within a program. The lesson introduces two rules that relate to issues of scope. The first is that variables defined as arguments to a function can only be referenced within the body of that particular function. This is illustrated by the following example. The variable introduced as the function argument, x, exists only within the scope of the function. Thus, any attempt to reference it outside of the function cause the program to crash.

f = (x)->
  see x

f("the argument") # prints "the argument"
see x             # throws a ReferenceError: x is not defined

The fact that a function's arguments exist only in the scope of that function is of immense importance to the language, as will become clear in subsequent lessons. Though the rule is simple, in practice give rise to many coding bugs, especially for novice coders. The What can go wrong section of these notes explores misapplications and misunderstandings of this topic in context.

The lesson's second scope-related rule is that variables defined outside of a custom function (in the enclosing scope) can generally be referenced inside the body of the function (in the local, or function, scope). This is a very convenient feature, as it means we don't have to explicitly pass a variable to a function for that variable to be referenceable from within the body of the function.

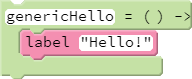
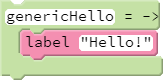
The lesson's coding snippet capitalizes on this second feature of scope in action (though how scope features into the workings of the example is not made explicit):

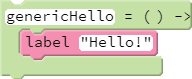
To appreciate how scope factors into the lesson's genericHello function, one must first recall that the label function is sprite-specific. Thus, the call to label is actually an alias to the call turtle.label. Note how we didn't need to pass turtle as a function argument for it to be referenceable (either explicitly or implicitly, such as through the call to label) from within the function. turtle.label is accessible from within the function definition because turtle exists in the enclosing scope.

These two rules are useful guidelines for beginners, but they are not the full story. There are several exceptions to this second rule about scope. These exceptions are critially important, however, as they significantly impact how scope is actually established, which in turn can dramatically impact how a program executes. These notes provide a more complete discussion of scope and its many nuances in the Beyond the Lesson section, below.

Documentation

In addition to assigning self-documenting names to functions, it is a good habit to preface function defintions with a brief description of their features and use. These notes should also describe the purpose and nature of the arguments, as illustrated here:

# draw a line from p1 to p2
# p1,p2 are arrays or HTML coordinates objects
drawLine = (p1,p2)->
  jumpto p1
  pen black, 1
  moveto p2 

A more formal mechanism for documenting functions in JavaScript is JSDoc. If you use JSDoc, many common integrated development environments (a.k.a., IDEs) can code and type hints, give warnings, highlight errors, and more. However, these features do not work in the Pencil Code environment. Interested readers are encouraged to further explore this topic on their own.

Notes to Activities

The Squares activity is intended as a simple warmup, but students who don't approach it methodically may get tripped up. A good starting point is the code to draw the centered square (a task previously tackled, in the Coordinates! lesson). Students might then turn to the task of coding a simple function that takes no arguments, and as a last step add arguments to enable the function caller to specify features such as sideLength or color.

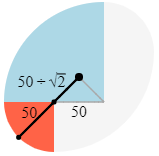
Ovals can be created using a variety of algorithms. The instructions suggest an approach that is perhaps computationally most simple. A few additional algorithms are illustrated in coding examples in this folder. Drawing the oval centered around the current location of the turtle is a bit trickier, but for students inclined to work through some basic geometry, it can be a satisfying accomplishment. The key to the required turtle movements is illustrated below:

In a number of the additional activities (below), such as RandomMoves and Writer, students are encouraged to pass a sprite as an argument to the function, in order to manipulate that specific sprite from within the function. An alternative solution is to write functions that can be accessed using dot notation, e.g., r.movetoRandom(). Formally, that type of function is called a method, and will be formally introduced and explored in a series of later lessons.

Additional Activities

• RandomMoves: code functions jumptoRandom and movetoRandom that relocate the default turtle to a random position on the visible screen. After you have succeeded at this basic function, define alternative versions that allow the function to be used with any sprite. To do this, specify a sprite as an argument to the function.

• CrazyLetters: Code a program to facilitate writing out strings in multicolored letters. Begin by writing a typeCrazy function that repeatedly prints a single letter, using the label function, but each time with a smaller fontSize and different color property. Then code a printCrazy function that takes a string and prints it to the screen using repeated calls to typeCrazy.

  
• Writer: Rewrite the Coordinates! lesson's Writer program to make use of functions. Your program should contain a function, drawLetter that takes an argument specifying a single string character for the desired letter which it then draws to the screen. You can iterate over a string of multiple characters using a for x in loop, e.g.,

  for letter in "a potentially clever phrase"
      drawLetter(letter)

  You will need to consider many logistical issues to complete this task. Perhaps the biggest challenge in this activity is defining the code for each of the 26 (or more) letters you might enter. Collaborating with peers—and divvying up the work—is probably a good idea!

  

  Given the many possible letters that can be passed to drawLetter, use of if/else can get tedious. A useful alternative in such cases is a switch statement, the usage of which is described in these notes at coffeescript.org. Also, simplify your effort by focusing only on uppercase letters. Note that any string can be converted to uppercase using the String class's toUpperCase method, e.g., "x".toUpperCase() or letter.toUpperCase().

• The StringArt activity introduced in the Coordinates! lesson focused on moving a sprite between successive sets of points. An alternative and arguably "cleaner" approach is to conceptualize the task as drawing successive line segments. To facilitate this, code a function drawLine that takes two array arguments, each of which represents the coordinates of an endpoint of a particular line segment. Use drawLine in a for loop to draw a StringArt design.
  

• MathPlots: Graphing data or displaying plots of mathematical functions is complicated by the fact that the coordinates that you want to plot usually won't match the coordinates of the Pencil Code environment. When plotting data, we will typically want to choose a different location for the origin (the center of a math graph, where the two axes meet) than the center of the screen, and we'll potentially want to use different scales for the x and y axes.

  The goal of this activity is to work through these graphing challenges. JavaScript functions will be central to this (and to subsequent improvements on this program in the next lesson). Functions will not only help make the coding task easier, but also make it easier to reuse this code in future work.

  

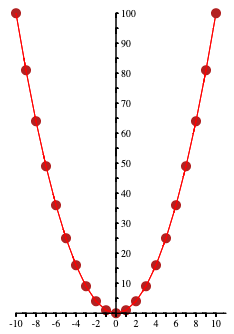
  Consider the simple example of plotting the curve y = x2 over the domain -10≤x≤10. For the purpose of discussion, consider the following first stab at this task.

  [w,h] = sizexy()
  speed 100
  minX = -20
  maxX = 20
  
  pen green, 1
  x = minX
  jumpto [x, x*x]   # this is the (x,y) coordinate
  for x in [minX+1..maxX]
    moveto [x, x*x]

  Copy the code to Pencil Code and run it. You will likely agree that the resulting graph is disappointing: it is tall and skinny and positioned too high on the screen. Our task is to improve upon this initial effort, by transforming the x and y values of the coordinates from the graph you would draw in math class (y = x2) to the x and y values needed to represent these points on the screen.

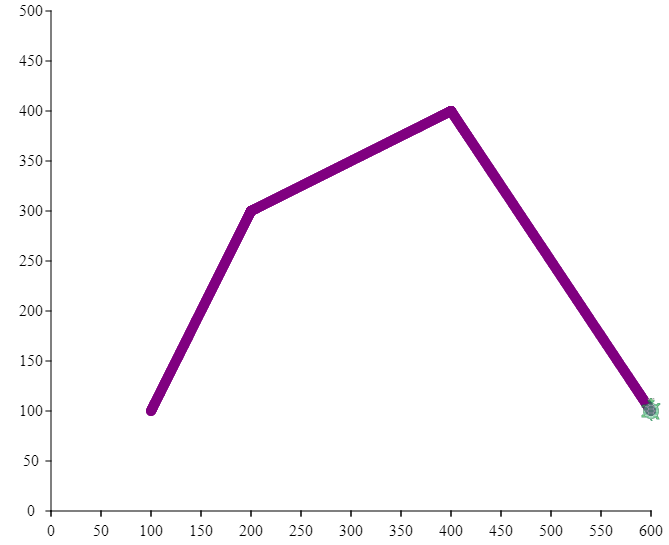
  Code two new functions, movetoT and jumptoT, which will function similar to Pencil Code's moveto and jumpto, except that they should take the coordinates that we would enter into our "math class" function (e.g., [2,4] or [10,100]), but move the turtle to an adjusted (or transformed) coordinate that result in output that looks good on screen. A call to moveToT(0,0) might position the turtle at the Pencil Code coordinate (0,-300). A call to moveToT(10,100) might position turtle at the Pencil Code coordinate (250,300). (The actual values will depend on how you code the program, and on your personal sense of aesthetics!)

  Tackle this work in stages. For example, you might first focus on scaling the x-values, based on the minimum and maximum x-values you wish to plot and on the actual width of the screen. Once you have solved this, move on to similarly scaling the y-values. As you progress through this activity, your output should evolve as illustrated in this example.

  Pass information to movetoT and jumptoT, such as the desired scale factors, minimum and maximum x and y values, and so on, using arguments. To simplify function calls, define default arguments for the Pencil Code coordinate for the location of the graph's origin and the scale multipliers needed to translate between the two coordinate systems. Default arguments are a coding feature described in the Beyond The Lesson section of this document,

  As a last step, add coordinate axes to your graph, using another function, drawAxes. However, adding labels can get quite tricky, so you might want to leave that task for another day!

• Dashes: create a variant of fd, called fdDashed, which instructs the turtle to draw a dashed line of a specified length. This function should take, as a minimum, three arguments: one for the distance over which to draw the dashed line, one for the dash length, and one for the sprite that should respond to the function call (as done in the RandomMoves activity, above).

  Teacher's note: this exercise has a reasonably low floor, but a potentially very high ceiling. For students inclined to work through the logic, encourage them to develop dash algorithms based on start and endpoints, so the dashes are evenly spaced. Another alternative is to have the dashes and spaces always equal, but make the end dashes fractional, so that dashes are otherwise consistent in length.

• UpdateArray: In a previous lesson, the push and pop (and unshift and shift) functions were introduced to add and/or remove values from an array. However, these function only allow us to add or remove from the end of an array. Later on, students will learn about other methods of the Arrays class that facilitate other manipulations of arrays, such as updating values and adding or removing values. In the meantime, in this activity, write a function insert that uses push/pop (or unshift/shift) to add a number to an existing array of numbers, in the correct position of ascending values. For example, if an array currently is defined as x = [5,8,9,12], then insert(x,10) should result in x having the value [5,8,9,10,12].

Beyond the lesson

Scope

Scope is a language feature that allows programmers to compartmentalize their programs, so that at different points of program execution, only a subset of all variables used in the entire program is currently accessible. More formally, scope describes the current context of execution in which variables can be referenced. If a variable or expression is not in the current scope, it will not be available to be read or written to. JavaScript scopes are layered in a hierarchy, in which child (or enclosed) scopes have access to parent (or enclosing) scopes, but not vice versa. Sibling scopes likewise do not share access with each other.

Prior to this lesson, all student work has been in the top level of the scope hierarchy, the global scope. The issue of scope arises in this lesson because every function creates its own scope, referred to as a function scope or local scope. Variables in the global scope (i.e, global variables) are by default visible everywhere, but variables assigned to a function scope (local variables) are visibile only in that function (which includes the scope of any function defined within that function).

Once one has a basic grasp of the hierarchial nature of scope, the primary challenge generally is correctly determining to what level of scope any specific variable will be assigned. This is complicated by the fact that, like most modern programming languages, JavaScript uses lexical scoping. This means that functions are executed using the variable scope that was in effect when they were defined, not the variable scope that is in effect when they are invoked. In plain English, that means that the placement of a function's definition in the broader program, with respect to other variables in that program, directly impacts the resulting function scope.

We consider several possibile scenarios involving scope, beginning with two which illustrate aspects of scope alluded to in the lesson and discussed in the More about the lesson section above.

Case 1: A variable used outside of and prior to a function definition can be accessed within that function.

In the following example, the global variable o can be accessed from within the local scope created by the call to the function f:

o = "o is a global scope variable"

f = ()->
  see o
  
f() # prints "o is a global scope variable"

The following more extensive example builds on the previous one, to illustrate that a value in the enclosing scope (the global variable o) can be modified by code in the function body:

o = "o is a global scope variable"

f = ()->
  see o
  o = "o is updated inside the function"

see o # prints "o is a global scope variable"
f()   # prints "o is a global scope variable" and updates o
see o # prints "o is updated inside the function"

In the preceding example, don't overlook the fact that the update to the global-scope (i.e., containing-scope) variable occurs when the function is called, not when the function is defined. Of course, this makes sense intutively, since the code in the function is not executed until that function is called.

The next example presents a scope-related outcome that is less intuitive, which illustrates JavaScript's lexical scoping structure: in order for the variable referenced inside the function to point to the variable in the enclosing scope, the variable must exist in the enclosing scope prior to the function declaration (i.e., when it is defined).

In the following snippet, the function that references o is defined prior to the declaration of o in the containing scope. As as result, a variable o is created within the local scope of the function. This variable is not accessible in the global scope.

f = ()->
  see o
  o = "o is updated inside of f"
  see o

o = "o is a global scope variable"
see o # prints "o is a global scope variable"
f()   # prints "undefined", updates the local scope 
      # variable o, then prints "o is updated inside of f"
see o # prints "o is a global scope variable"

Case 2: A variable listed as an argument in a function definition can only be accessed from inside that function.

f = (a)->
  see a

f("example") # prints "example"
see a        # throws ReferenceError: x is not defined

Though this second rule is straightforward, it is a feature of suprising importance in JavaScript, as it underlies many advanced coding idioms which will be explored in subsequent lessons. At this point, the primary benefit of this feature to students is that it provides a way to guarantee that a variable in a function has local scope, which means the variable can be modified without impacting a variable by the same name in the enclosing scope (which, if done inadvertently, would result in a coding bug).

The following snippet illustrates this second rule in practice. The key takeaway is that when the function is executing, there are simultantiously two variables named o, one in the function scope, and one in the global scope:

o = "o is a global scope variable"

f = (o)->
  see o 
  o = "o is updated inside the function"
  see o 

see o # prints "o is a global scope variable"
f()   # prints "undefined", updates o,
      # then prints "o is updated inside the function"
see o # prints "o is a global scope variable"

The trick to ensuring the local scope variable is distinct from the global scope variable of the same name is including it as an argument in the function definition. By this second rule, this guarantees that a local scope variable is declared. Note that this works even if, as in the example, we do not pass a value to the function when invoking it. The variable is declared each time the function is called; in our example, the value is then subsequently assigned a value in the body of the function.

This situation of simultaneously having two (or more) variables with the same name exist in different scopes within a single hierarchy (e.g., parent-child) is termed variable shadowing. Used inadvertently, it can be the source of coding bugs, but used intentionally, it ensures that function-level variables do not get confused with enclosing-scope variables.

Introducing variables as function arguments is the only sure-fire way to ensure that we don't mistakenly code a namespace collision, a situation in which a variable referenced in a function is (unintentionally) the same as one already declared in the containing scope.

The following script shows how easily a namespace error can sneak into a program. The code successfully creates a local-scope variable sum (by listing it as an argument to the function f), thereby avoiding a namespace collision with the global variable by the same name. However, the variable i used as an index in the embedded for loop was overlooked. As a result, the reference to i in the function body overwrites the global-scope variable i:

i = "a global scope variable"
sum = "a global scope variable"

f = (sum)->
  sum = 0
  for i  in [1..3]
    sum+=i
  see sum
    
f()      # prints the value "6"
see sum  # prints "a global scope variable"
see i    # prints "4", the result of a namespace collision

Case 3: A variable assigned a value in the body of a function but not in the enclosing scope does not exist in the enclosing scope of that function.

This observation, illustrated in the following snippet, simply notes that if you make an assignment to a variable in the body of a function, but do not make an assignment to the same variable name higher up the scope hierarchy (e.g., in the enclosing scope), then a variable with that name will be created with in the scope of that function. This variable will not be accessible in the enclosing scope; attempts to reference it will cause the program to crash.

f = ()->
  i = "i is a local scope variable"

f()
see i # throws ReferenceError: i is not defined

Default args

Functions can be defined so that arguments take default values, as done for the following alternative to the drawPolygon function.

The call drawPolygon(3) will now produce a randomly-colored triangle with side length of 1000/3. The same function can also be used to generate a blue square with side length 250 (by executing drawPolygon(4) ), a green pentagon with side length 200 (via drawPolygon(5, green) ), and so on. Default values can be overridden, but they must be overridden in order. Thus, in the preceding example, to override the default color, values for sides and sideLength must be specified explicitly, e.g., drawPolygon(5, 200, blue).

random(6)          # return a whole number less than 6

random([1..10])    # return an integer in the set [1,10]

random(1,10)       # return an integer in the set [1,10)

random("normal")   # return a value from the standard 
                   # normal distribution

random("position") # return a HTML coordinate from the 
                   # visible screen

random()           # return a value in the set [0,1)

Effective argument evaluation can require the use of advanced language features, such as error handling. However, conditional logic will suffice in most situations, in particular in conjunction with the typeof function. typeof returns a string that identifies the data type of the value represented by that variable. Using typeof, we can evaluate the data type of an argument prior to using them in computations, and thereby avoid using them in a way that might cause our program to crash.

The drawPolygon function below illustrates the use of typeof for argument evaluation. Calls to drawPolygon can include both a string (for a color) and a number (for the number of sides), in either order. The function also provides default values if either the string or the number (or both) are not provided.

Refer to the Technicalities section of this document for a further exploration of argument evaluation and related topics.

Unintended side effects

If in accomplishing its intended task, a function leaves the program in a state different than it was prior to the function call, that function is said to have a side effect. Of concern is when there are unintended side effects. Common examples of unintended side effects that may arise this lesson's coding activities are changes in the status of pen (changing the color and/or it's up/down status) and changes to speed.

Additional activities in the Notes to the Callbacks! lesson provide students opportunities explore advanced techniques to avoid side effects involving pen status and speed. At this point in the curriculum, students can simply work around such side effects by (re-)setting the pen or speed settings as desired after the function call. However, in more involved programs, and in particular when designing functions for broader use (such as part of a publically-shared library), coders should strive to eliminate unintended side-effects or, at a minimum, to document those that cannot be avoided.

Topics for upcoming lessons

Functions serve many other purposes beyond those introduced in this lesson. They can be used to get information from an object (e.g., getxy) or to change the state of an object (e.g., jumpxy). They can be used to carry out and return the results of computations (e.g., distance, Math.abs). Writing functions is also a necessary step to using Pencil Code features such as buttons and the forever function, and for CoffeeScript features such as defining classes, which are themselves special types of functions. This represents a lot of material, some of which is conceptually challenging. Many of these features will be explored subsequent lessons, including:

• return statements: The focus in this lesson is on functions that "do" something, like carry out an animation. Of course, functions have much broader usage than this. For example, functions can carry out computations and return a result. That aspect of functions (which involves return values) will be discussed in the next lesson.
• callbacks: A common coding idiom is to create a function with the purpose of passing it to another function, which then invokes it at some later point. Examples of such callback functions abound in Pencil Code. In the statement await done defer()—discussed at length in the Notes to the Array Destructuring! lesson—the function done accepts a callback function, provided by the call to defer(). Other Pencil Code functions that take callback functions as arguments include read, readnum, forever, button, click, keydown, listen, plan, load, and loadscript. These functions will be introduced subsequent to the Callbacks! lesson, opening up a vast range of additional interactive coding possibilities.
• first class functions: A programming language is said to have first class functions when functions in that language are treated as any other variable. In JavaScript, functions are a special type of object. They are special because they are callable. But the fact that they are objects means that funtions can be assigned different names, added as properties of other objects, and passed as arguments to other functions—i.e., they are first-class in nature. The Writer activity, above, provides an example of how useful this feature can be. It uses functions to draw each specific letter, and passes these functions to another function, drawLetter, to write out words. First-class functions are discussed further in the Notes to the Callbacks! Lesson lesson.
• anonymous functions: In this introductory lesson, functions are assigned a specific name, and that name is subsequently used to invoke the function. However, in some situations, a function definition is needed only once, perhaps most notably when functions are used as callbacks. In such cases, it is common to define and invoke a function without giving it a name, i.e., anonymously. This features is explored in the Mouse Events! lesson.
• methods: The current lesson simplifies things by focusing on manipulating a single sprite, the default turtle, within each function definition. In a discussion of function arguments, these notes describe how to pass sprites as arguments, which remove this single-sprite limitation. An obvious extension is to make functions work with dot-notation, such as the built-in rt and lt functions. When functions are added as properties of objects, they are more accurately called methods. Coding methods involves a deeper understanding of variable scope and other issues, which will be explored in the Methods! lesson.
• closures: JavaScript's lexical scoping structure makes it possible to use nested function calls to create a variable within a function that continues to exists even after a function has completed execution. This clever, useful idiom is discussed in the Closures! lesson.

What can go wrong

Functions are central to the JavaScript programming language, essential for many powerful coding idioms. The Custom Functions! lesson is intentionally limited in breadth, in order to avoid overwhelming students with too much new content and to sidestep areas that are more likely to lead to excessively technical or difficult coding challenges. So long as students "keep it simple" in their current efforts, they should not have too much trouble. However, given the nuances of working with functions, errors are certain to arise.

Animation queue

Given the lesson's emphasis on manipulating sprites from within functions, students may run into complications involving the animation queue. Problems with the animation queue frequently become particularly pronounced when custom functions are used in programs that involve multiple sprites. In short, timing issues can get difficult to work through. The timing of calls to sync may be difficult to work out. Moreover, calls to await done defer() within function often do not work as desired.

Calls to await done defer() are typically made to correctly time execution of functions that aren't included in the animation queue, such as getxy. In such cases, the (sprite-specific) plan function provides an alternative means to get the desired results, without the drastic impact on the execution of the program caused by await done defer(). See this script for an example of problem code and a corresponding workaround using plan. Use of plan will be explored in the Notes to the Callbacks! lesson.

Unspecified arguments

When a function that is written to expect an argument is not passed a value when called (and assuming that no default value was not provided for this argument in the function definition), JavaScript sets the type of the argument variable to "undefined" and its value to the special data value undefined. Depending on how the variable is referenced in the function, this reference to undefined can cause the function to fail or yield other unexpected results.

As an example, the following snippet, which crashes when run:

Pencil Code provides an error message, shown below, which correctly identifies the problem, though students will likely to find the message hard to interpret:

The message Pencil Code is trying to communicate is this: because no value was passed to the function when the function was called, the variable t was set to undefined. JavaScript throws a TypeError because data values of type undefined do not have a label property. This unchecked exception causes the program to crash.

Note that many built-in Pencil Code functions are written to accept a wide variety of arguments (including none at all) and therefore typically they don't cause the program to crash when invalid arguments are passed to them. For example, calls to pen with invalid arguments, such as pen turtle or pen "mistake", revert to a default color and width, as if pen black, 1 had been called.

As students become more experienced writing functions, encourage them to write functions that anticipate user error, much like the built-in Pencil Code functions do.

Several workarounds can be incorporated into custom function definitions to make them more robust and thereby help avoid potential runtime errors. One of the easiest approaches is to specify default values for arguments, as illustrated in the following example, which specifies turtle as a default value for the argument t. This version of genericHello will run without a hitch when no value is passed to it.

Alternative approaches to avoiding argument-related errors when functions are called include argument evaluation, described above, and error handling, the topic of a later lesson.

Scope-related errors: referencing args outside of functions

Given the complexities involved with variable scope, there are several scope-related errors that are certain to eventually appear in student work. One easily-avoided, yet common coding error is attempting to access a function's arguments outside of the scope created by a call to that function. The following snippet provides a simple example of how this type of error may arise.

doubleTheInput = (x)->
  x*=2

y = 5
doubleTheInput(y)

see y # prints "5"
see x # throws a ReferenceError: x is not defined

As its self-documenting name describes, the logic of the doubleTheInput function is that it doubles the value passed to it, which it in fact does. However, the mistake is in thinking that the value of the variable (y) referencing the value that was passed to the function (5) was updated as well. It is not. The variable that is updated is a function-scope variable x, which only exists within the body of the function.

This result may seem arbitrary and/or unnecessarily restrictive, especially when presented in an example such as the one given above. However, put in the appropriate context, and when students have learned a little more about functions, the result should come to be seen as intuitive.

To support this argument, it is helpful to introduce the concept of return statements, a topic to be formally introduced in the following lesson. return statements provide a means to pass a value computed in a function—in our example, twice the value of value passed to the function—back to the main body of the program.

In the following snippet, the doubleTheInput function has been modified so that it explicitly returns a computed value. (It does not ever bother to modify the variable x, as doing so clearly serves no purpose.) With this design, there now is no reason to want to access the function argument, x, outside of the function.

doubleTheInput = (x)->
  return 2*x

y = 5
doubledY = doubleTheInput(y)

typeline doubledY # prints "10"

Upon reflection it should become apparent that there is no logical reason to try to access, outside of a given scope, a variable that is introduced as an argument to the function that created that scope. To convince yourself of this, consider the built-in Pencil Code function fd. The desire to access a function argument outside of the function is akin to executing the statement fd(100) and subsequently wanting to access the value passed to the function (i.e., 100) by referencing the variable name used for that argument in the definition of the function. For starters, we already know the value we passed to the function! Moreover, and more importantly, we aren't privy to the inner workings of fd, so we do not know the name by which to reference the value anyway.

In sum, students may misperceive the variable scope rule that states that a variable introduced as an argument in a function definition can only be accessed from inside that function, to be a limitation of the language. However, the only limitation at play here is that the thing you should never need to access is not accessible—which is to say it's no limitation at all.

Scope-related errors: namespace collisions

Accessing variables from the containing scope from within a function definition is convenient. However, doing so can increase the likelihood of subsequent coding bugs, particularly in larger programs. The most likely pitfall is that the variable from the enclosing scope may be unintentionally changed from within the function. The likelihood of this happening is greater for variables with generic names, such as i or x and y that may refer to separate indexes or be used to track different sets of coordinates inside and outside of the function definition.

As an example, consider the following script, which is intended to draw randomly-sized rectangles at random positions on the screen. However, when it the script runs, most of the random rectangles are clustered at the center of the screen, rather than spread out.

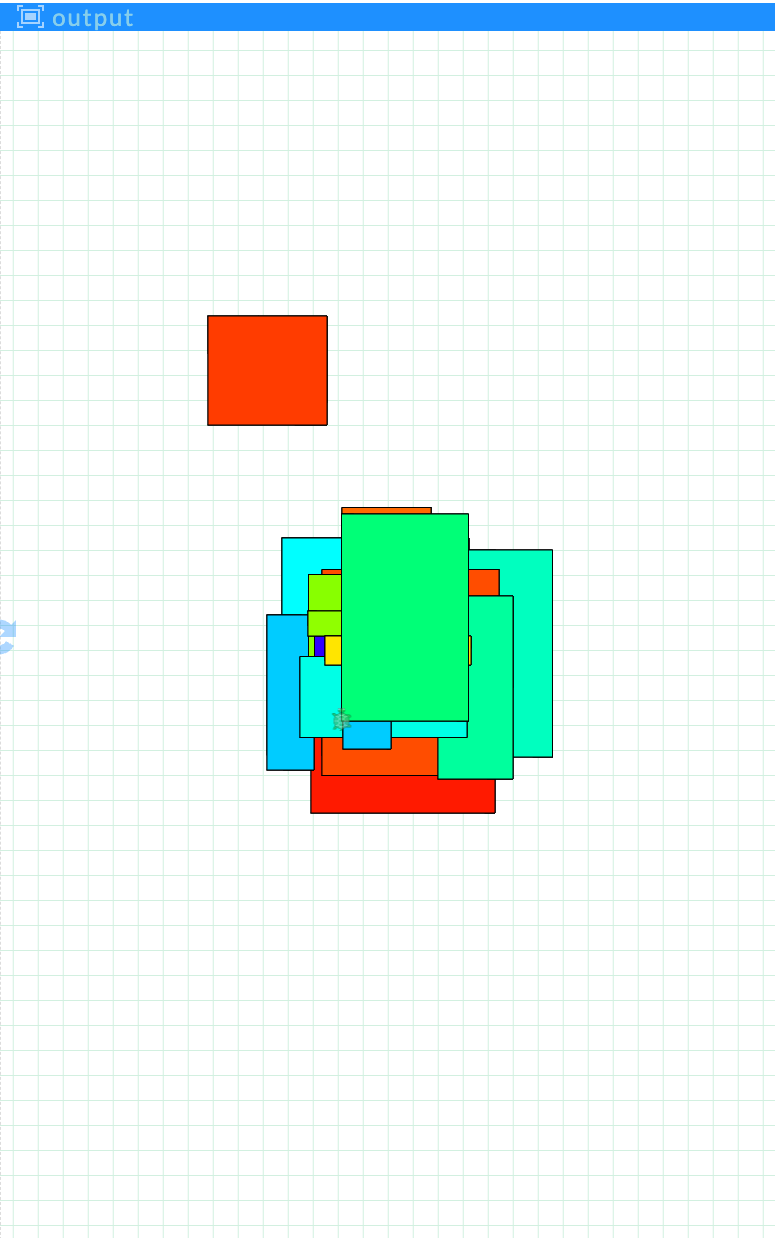
The code does not function as intended because the values w and h of the containing scope (defined on line 25 and referenced again in lines 44 and 45 to position the rectangles), are overwritten in each call to drawRect (on line 48). That is, the assignments to w and h within the body of drawRect (lines 32 and 33) overwrite the global variables, because they have global scope. As a result, all but the first rectangle are positioned very close to the center of the screen: their coordinates on screen are based on the dimensions of the previous rectangle rather than the page dimensions.

The variables within the body of the function have global scope because the variables existed prior to the definition of the function and because the variables were not intentionally defined to have local scope in the definition of the function.

The lesson notes that variables defined outside of a function by default are accessible from within that function, but as these notes make clear, there are exceptions. The most hard-and-fast exception to this rule occurs when a variable introduced as the argument to a function has the same name as a variable in the containing scope. This situation, called variable shadowing, results in two distinct variables with the same name, one being in the enclosing scope (i.e., from where the function was called) and the other existing locally in the function scope. Within the function definition, references to the named variable will be to the value passed to the function, via the argument, in the function call.

The risk of both of the variable-related pitfalls described in this section can be mitigated through explicit use of arguments to pass information to a function. It is considered good style to rely on function arguments as much as possible to pass information from the containing scope to the function, rather than referring to variables in the containing scope directly.

Admittedly, for students new to custom functions, these issues are excessively nuanced and, moreover, unlikely to surface early on. It is largely in the interest of preventing bad habits from developing that students should be encouraged to use arguments to pass information to functions whenever possible. Thankfully, "doing it right" does not entail much additional work. For example, and as illustrated previously, the lesson's example of genericHello (which implicitly references the global scope turtle variable) can be modified so that a specific sprite is passed explicitly to the body of the function, as illustrated below.

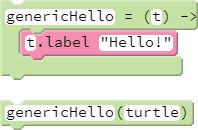
An extra benefit in this example is that the function can now be used with any sprite, not just the default turtle.

Pedagogy

Computational thinking

Functions are a particularly useful addition to a developing coder's toolbox. They offer much more than just a way to get code organized or to simplify code maintenance. Echoing a common refrain in the learning sciences, that "tools mediate thinking," use of functions encourages thinking about logic challenges in a different way.

Learning to code requires picking up some syntax and memorizing various functions and operators. However, coding involves so much more than this. Ultimately, we want students to tackle larger problems by breaking them down into smaller, meaningful pieces (decomposition) and thinking in terms of more general concepts (abstraction), thinking through the step-by-step instructions needed to accomplish a particular task (algorithmic thinking), and identifying patterns that they can harness to simplify algorithms (pattern recognition). Together, this "different way of thinking" is known as computational thinking

Technicalities

Terminology: "arguments" vs. "parameters"

A variable defined in function declaration is formally referred to as a parameter. An argument is the actual value of this variable that get passed to the function. In the coding snippet in the lesson, name is the parameter, and "you" is the argument passed to the function.

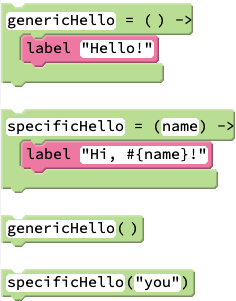
This curriculum does not highlight the distinction between the concepts of parameter and argument. It chooses instead to use the common-parlance use of "argument" as a catch-all for both. Making the distinction typically adds little value pedagogically, yet can be a source of additional confusion.

That said, there are a very few situations in which it is expecially useful to draw a disctinction between parameters and arguments, and in such cases, these notes will draw on that. One example appears below, in the dicussion of the JavaScript reserved word arguments.

Data type of functions

Functions are a special class of the JavaScript object data type, but they have an additional feature: they are callable, which means you can tell the interpreter when you want to execute the statements that it contains.

Argument evaluation/validation

JavaScript lacks a built-in mechanism to automatically test whether arguments passed to functions match the data type intended by the author of the function. For example, a function may be written with the expectation that a numeric value be passed to it as an argument, but in the script that contains the actual function call, a value of any data type can be passed to it. Another example is that a function written to have an argument passed to it may be called without actually passing a value.

This aspect of the JavaScript language stands in stark contrast to the workings of strongly-typed languages such as Java. In strongly typed languages, each variable is declared as a specific variable type that cannot change over the course of the program. This design feature impacts a language in myriad ways. One impact on functions typically is that both the number and type of variables passed as arguments to a function must to match the number and type of variables specified in the function definition.

While JavaScript's weakly-typed structure can lead to a host of runtime errors, as incompatible data types are passed to functions, it also provides a vastly increased level of flexibility. This flexibility is clearly evident in Pencil Code itself. Most built-in Pencil Code functions take advantage of JavaScript's weak variable typing to permit the user to omit arguments in the function call, or even provide invalid arguments, and yet (though the results may sometimes be surprising) the function can still excecute without resulting in a runtime error. For example, dot blue makes a blue dot with a default size of 10, and both dot() and dot turtle produce a black dot with diameter 10.

JavaScript provides coders two important options to avoid problems associated with function calls. First, they can build in error handling, a language feature that will be introduced a later lesson. The second option, introduced above, is to evaluate arguments based on their data type, prior to carrying out calculations using the value of those arguments. The remainder of this section expands upon that earlier discussion.

Two language features key to utilizing Javascript's flexibility in function arguments are the built-in typeof function and arguments parameter.

As noted previously in these notes, the typeof function is key to processing arguments data without incurring a runtime error. It is especially useful because every variable has a type—even variables that have not been assigned a value and therefore would seem to have no type! In such cases, the data type is the special type "undefined".

Consider first the following example using the typeof function:

This function explicity tests whether values have been provided that match the expected variable type for each variable. typeof returns one of six values: "object", "boolean", "function", "number", "string", and "undefined". Note that these return value are all strings, i.e., the quotes are required, and that any argument not passed in the function call is assigned a value of undefined and therefore has type "undefined". Whenever arguments provided by the caller do not meet the expected form, then default values are employed.

The use of typeof here is typical: to evaluate the type of the variable, before that variable is evaluated further. For example, sideLength<0 is only tested after it has been established that sideLength has type "number".

JavaScript's built-in arguments parameter provides even greater potential to evaluate values passed to a function (including establishing that no values were passed at all). The arguments parameter is available in every function; in fact, arguments is Javascript reserved word, so the system-provided values cannot be overwritten.

arguments is an Array-like object that contains the values of all arguments passed to that function. Rather than specify any specific arguments, a function can be written to iterate over this default collection, and pluck out data according to the nature of the data passed, using conditional logic.

The drawSquare function in the following example has no explicit arguments in its definition. It illustrates how a function can be defined to rely on the arguments parameter rather than specifying the arguments as described in the lesson.

The ? operator

In CoffeeScript, the question mark symbol (?) functions as a boolean operator that tests whether a variable exists or has been assigned a value of undefined or null. The ? operator can be used in two ways. The first is as a unary operator, such as in the following example:

if not x? 
  # declare x and assign it a value of 100 if x is undeclared, 
  # or set x to 100 if x exists and is undefined or null
  x = 100

CoffeeScript's ? can also be used in a binary fashion. x ? 100 returns the value referenced by x unless x is undeclared, null, or undefined, in which case it returns 100. Using ? in this fashion, the following one-liner accomplishes the same result as the previous example, but without the need to use an if statement:

x =  x ? 100

Pay careful attention to the syntax in the preceding examples. When used as a unary operator, ? must follow the variable name immediately, without a space. When used as a binary operator, ? must be buffered by spaces.

CoffeeScript's ? operator is very convenient alternative to more cumbersome or advanced error-handling techniques. For example, it obviates the need to use try/catch to detect undeclared variables. In the context of this lesson, ? is useful in function definitions, as it provides a convenient means to test whether a value specified as a parameter in the function definition has actually been called with an argument for that parameter. The following example uses the binary syntax of ? to provide a default value for the argument x:

doubleTheInput = (x) ->
  x = x ? 0 # set x to 0 if no value provided in function call
  return 2 * x

see doubleTheInput()    # prints "0"
see doubleTheInput(100) # prints "100"

JavaScript also has a question mark operator, though it's usage differs from CoffeeScript. In JavaScript, ? provides a convenient means to express an if/else statement in one line of code. The JavaScript ? takes three operands (and for this reason is often referred to as the ternary operator): a condition, a value returned if that condition is true and a value returned if that condition is false.

Recall that the backtick operator can be used in CoffeeScript programs to execute pure JavaScript statements. The following statement with the ? operator is equivalent to the subsequent if/else:

# JavaScript Code embedded in CoffeeScript program
`var outcome = random() > 0.5 ? "heads" : "tails"`

# CoffeeScript equivalent
if random() > 0.5 
  outcome = "heads"
else
  outcome = "tails"

Method overloading

The flexibility in using arguments described in the previous section should not be confused with method overloading. Method overloading a feature of some strongly-typed programming languages, such as Java, which makes it possible to create multiple, distinct functions that share the same name. This is made possible by the fact that Java identifies functions based not just on their name, but on their signature, which includes the number, type, and order of arguments. Being a weakly-typed language, JavaScript does not incorporate method overloading. No two functions can share the same name. However, as illustrated in the preceding paragraphs, JavaScript's flexibility with function arguments provide an alternative means to accomplish somewhat similar results, i.e., we can write a single function definition which can be used with different configurations of arguments.